Let’s locate the orbital periods of the planets on a slide rule, and from this find out how long it takes to travel from Earth to Mars. We can do this!
Kepler’s Third Law
Kepler’s Third Law of celestial mechanics tells us that the square of the period of a planet’s orbit is proportional to the cube of the orbit’s semi-major axis. The orbits of the planets are elliptical, but for the most part their eccentricity is small, rather resembling circular orbits to good approximation. For this case, Kepler’s Law can be obtained by comparing the centripetal force on a planet of mass m circling the sun at speed v = 2𝜋R/T with the force due to the sun’s gravity:
One may not have the values of Newton’s gravitational constant (G) or the mass of the sun (M) at hand, but we do know that the semi-major axis of the earth’s orbit about the sun is one astronomical unit (by definition) and that it takes one year for the earth to revolve once through its orbit (by definition). So, our “constant” must have a value of 1 cubic AU per square year. If we know the radius R of a planet’s orbit in units of AU, then we can use the above ratio to estimate its orbital period T in Years:
Cubes and square roots are natural operations to perform on many basic slide rules. But can we easily find the distances from the Sun to each planet in Astronomical Units? Enter Bode’s Law…
Bodes Law
The orbital radii of (most of) the planetary orbits in our solar system roughly obey a relationship referred to as the Titius-Bode’s Law — more commonly known as just Bode’s Law — which is named after the German astronomers Johann Daniel Titius and Johann Elert Bode. (Titius reported on this relationship in 1766, then Bode referred to Titius’ work in a document in 1772. This is how things go sometimes…) The “law”, good to a couple of digits accuracy, goes something like this:
from which R provides the approximate orbital radii for the celestial bodies of the solar system. The result yields the following table for the planets known in the 1770s, noting that there appeared to be a “gap” in the law at n=3:
Approximate Orbital Radii (AU)
n a=3*2^n Planet R (Bode) True
- Sun 0.0 0.0
- 0 Mercury 0.4 0.387
0 3 Venus 0.7 0.723
1 6 Earth 1.0 1.00
2 12 Mars 1.6 1.52
3 24 -- 2.8 --
4 48 Jupiter 5.2 5.20
5 96 Saturn 10.0 9.58
6 192 19.6
7 384 38.8 The “True” column gives the values of the semi-major axes of the actual elliptical orbits as they are known today.
When Uranus was discovered in 1781 at a distance of 19 AU, it also seemed to obey the Law. And following that result, Bode proposed, as had Titius, the existence of a “planet” at the gap at 2.8 AU. This turned out to be the asteroid Ceres (and the rest of the asteroid belt), discovered in 1801, bringing notoriety to Bode and his “law”. Note, however, that Neptune, discovered in 1846, somehow got thrown into the middle of all this and doesn’t respect Bode’s relationship at all. But Pluto — discovered in 1930 and now no longer regarded as a planet — falls back in line with Bode. A more complete modern table would be:
Approximate Orbital Radii (AU)
n 3*2^n Planet Bode True
- Sun 0.0 0.0
- 0 Mercury 0.4 0.387
0 3 Venus 0.7 0.723
1 6 Earth 1.0 1.00
2 12 Mars 1.6 1.52
3 24 (asteroids) 2.8 2.77
4 48 Jupiter 5.2 5.20
5 96 Saturn 10.0 9.58
6 192 Uranus 19.6 19.22
Neptune 30.07
7 384 Pluto 38.8 39.48
8 768 77.2 ?While there is no totally accepted theory as to why Bode’s Law works as well as it does (and, as we see, it doesn’t always work), nonetheless it is a fairly easy way to remember how to produce the distances to the planets in Astronomical Units.
Back to Kepler
OK, so back to our original question: What about the orbital periods? Now that we have orbital radius information in units of AU, let’s set up our slide rule calculation of the quantities
for the various planets. Do you have a slide rule with an A scale and a K scale? If so, you’re already set. In fact, if both scales are on the stock (the normal configuration) then we don’t even have to use the slide at all! As the A scale is the square of the D scale and the K scale is the cube of the D scale, then the solutions to our problem are already present, right in front of our eyes. And if you don’t (yet) have your own slide rule with the required scales, below is an image of one that happens to have a K scale immediately above the A scale.
Note that if the cursor is placed at an arbitrary value on the A scale, then the square root of this value is found on the D scale. And the cube of the number on D is found above on K. So, the number on K is the cube of the square root of the number on A. Just what we want for examining Kepler’s Third Law!
For instance, we can see on the slide rule that if the Earth’s orbit has a radius of 1 AU (set on the A scale) then its period is 1 Year (on K) — the 1 on A lines up with the 1 on K. Then finding the orbit of Mars at 1.52 AU (using the accepted value) on the A scale indicates an orbital period of about 1.88 Years as found on the K scale. (See next image, below.) Jupiter, at 5.2 AU, has a period of 11.9 Years, and Saturn, at 9.58 AU, has a period of 29.5 Years.

On the second half of the A scale we can line up the other outer planets. For Uranus, Neptune, and Pluto — at 19.2, 30.1 and 39.5 AU — we get periods of 84.0, 165, and 248 Years, respectively.
For the inner planets, where the radii are less than 1 AU (0.387 and 0.723 AU for Mercury and Venus), we need to think about how to use the scales to get the right answers. If we imagine the A scale as not going from 1 to 100, but rather from going from 0.01 to 1, then we can move the cursor to 38.7 or 72.3, which fall on the second half of the A scale, and note that the numbers are divided by 100, giving 0.387 and 0.723. But if A is divided by 100, we must also divide the results on the K scale by 1000. The situation is depicted below:
K: 1 - 10 - 100 - 1000 or 0.001 - 0.01 - 0.1 - 1
A: 1 - 10 - 100 or 0.01 - 0.1 - 1With this in mind, when we set the cursor to 38.7 or 72.3 on A, then we can interpret the readings on K for the inner planets as 0.242 and 0.615 Years for Mercury and Venus, respectively, as shown in our next image.

A tabulation of our results is shown here:
Approximate Orbital Radii and Periods
(derived from measured R values)
Planet R (AU) T (Years) True
Mercury 0.39 0.242 0.241
Venus 0.72 0.617 0.615
Earth 1.00 1.00 1.00
Mars 1.52 1.88 1.88
asteroids 2.77 4.61 4.60
Jupiter 5.20 11.9 11.9
Saturn 9.58 29.5 29.4
Uranus 19.2 84.0 84.0
Neptune (30.1) (165) 165
Pluto 39.5 248 248And there we have it! The A and K scales directly compute Kepler’s Third Law.
The fact that our computed values on the slide rule agree extremely well with the accepted values (“True” in the above table) should not be a surprise. It is very much easier to measure the orbital periods of the planets from years of data than it is to actually measure the orbital distances directly (or indirectly). So, in fact, Kepler’s Third Law is used in practice to compute the semi-major axis distances using orbital period measurements. Hence the fine agreement in this table.
A Trip to Mars
So, what about traveling to Mars? We will assume that a space craft is launched, uses its engines to obtain an appropriate velocity, and then coasts from then on, letting gravity do the work. To obtain a “minimum energy” trajectory, we wish to launch the ship onto an elliptical orbit that has a minimum distance from the sun that is the radius of the Earth’s orbit, and has a maximum distance from the sun that is the radius of Mars’ orbit. While we won’t derive it, we’ve noted that Kepler’s Law still holds true if the planetary orbits are elliptical and not exactly circular, if we interpret R as the semi-major axis of the ellipse in question. So, with an appropriate velocity when launched from Earth, the ship is sent on an elliptical orbit with a semi-major axis whose value is
and if we launch the ship at just the right time, we can leave the vicinity of the earth and arrive in the vicinity of Mars after a time T/2, where T is the full orbital period corresponding to a. The situation is depicted in the image below and is described further in its caption.
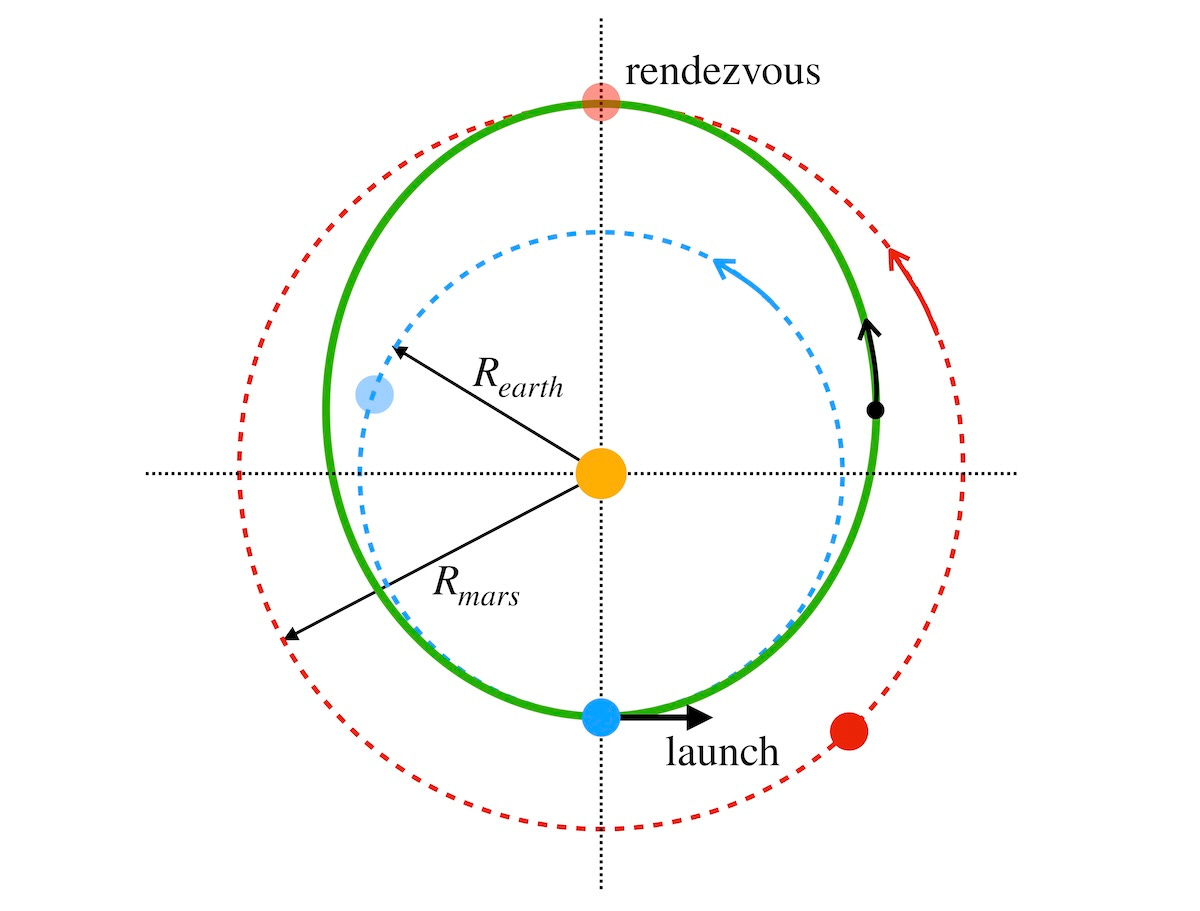
From the figure above and through the use of our table, we see that a = (1 + 1.52)/2 =2.52/2 =1.26 AU. And from the K and A scales, we see that if we set 1.26 on A we find a value of 1.41 Years on K for a full orbital period.
Hence, the time to go from Earth to Mars would be half of that value, or 0.705 Yr — that is, about 8.5 months. And of course we would like for Mars to be there when the ship arrives! So, we would need to launch the craft 8.5 months before Mars reaches the point opposite the sun from where the Earth was at launch time. (Refer to our earlier figure.) As you can imagine, this alignment only occurs every so often, and hence we can’t just launch a mission to Mars at any time. Rather, a narrow “launch window” occurs when these conditions are just right, or very nearly so. During the flight, the earth will go through 70.5% of a full cycle, or about 254 degrees of a full ( approximately circular) orbit while Mars, on the other hand, will go through about 135 degrees of its orbit:
which can be easily verified on, say, a slide rule.
And, of course, one would then have to wait until things line up properly again so as to launch from Mars and arrive at Earth. This requires about a 16 month wait for the astronauts on the planet, as it turns out. The initial placements of the planets for the trip home will be a little different, of course, but the time of flight essentially would be the same. Hence, a bare minimum round trip visit to Mars would take about 2 years and 9 months.
And so we’ve accomplished our mission, and have computed some important aspects of a space flight to Mars on a slide rule. And we didn’t even need to use the slide!







Fantastic article. Thank you for posting. I followed along with my K and E decilon, but I could have used my Aristo Scholar Nr 903
Excellent post, fun problem!