Creating a standard logarithmic scale as found on a slide rule is actually quite straightforward when access to values of logarithms is provided. As multiplication and division of numbers are turned into addition and subtraction of logarithms, we just need a scale where the placement of numbers is proportional to the logarithms of those numbers. This way, when we add distances along the scale, or on a pair of scales, that correspond to x1 and x2, in reality we are adding the logarithms of those numbers to get log x1 + log x2 = log (x1 × x2). When we want to do more than just multiply two given numbers together, such as multiply by a square or square root, divide by the tangent of an angle, or take a result and apply some other function to it, we can do so on a slide rule with a proper scale layout. But how are those scales created? In what follows we will discuss a procedure to do just that, first by examining the common Mannheim slide rule scales, and then building upon that to look at more of the standard scales found in the late-20th century slide rules.
The Standard Logarithmic Scale
We know that log(1) = 0. And we know that log(10) = 1. So these can form the endpoints of our standard logarithmic scale. Suppose we draw a line of physical length L0, where we make a mark and write a 0 at the beginning of the line, and make a second mark and a 1 at the end of the line. A common value of L0 might be 25 cm, or roughly 10 inches. We can divide the scale into 10 equal parts, as shown in the top line of our figure below, which has 0.05 subdivisions. Next, below this line, we draw a second line of the same length. This line will have labels that start at 1 (= 100) and end at 10 (= 101). To make marks for other numbers x between 1 and 10,
find log(x) for each x, perhaps from a table of logarithms. For example:
log(2) = 0.301, log(3) = 0.477, log(4) = 0.602, log(5) = 0.699,
log(6) = 0.778, log(7) = 0.845, log(8) = 0.903, and log(9) = 0.954.
place the mark for the number x opposite the value of log x, shown here, for x = 3:
For any given number between 1 and 10, we can mark its value on the x scale at a distance L0 × log(x) to the right of the “1”. In the figure above we show intermediate marks at 1.5, 2.5, and so on. But the divisions can be as fine as practical, with all being placed on the scale by multiplying L0 by the log of the numbers in question.
And so, with two such scales that can be moved with respect to each other, we can add logarithms to perform multiplication:
The values being added on the log x scales can be verified from our list of logarithms provided above: log 2 + log 3 = 0.301 + 0.477 = 0.778 = log 6. Once the scales are laid out, we no longer need access to the actual values of the logarithms. We can just line up the numbers on our x scales and read off the results of multiplications straight away.
Creating the Mannheim Scales
In 1850 Victor Amédée Mannheim of France created a new arrangement which is composed of four equal-length scales, which had the customary labels A, B, C, and D in his French patent, as used here:
We see that C and D are 1-decade long, marked from 1 to 10, while the A and B scales are still 2-decades long, marked 1 to 100. The central B and C scales slide together, while the A and D scales remain stationary. The length of a decade (1-10 or 10-100) of the A/B scales is half the length of a decade on the C/D scales. As such, under the numbers y on A we find “√y” on D, with the same relationship between B and C.
But how do we make our marks to create the A and B scales? They are both still logarithmic, but run from 1 on the left to 100 on the right. So suppose we want to make marks at values y, for example at y = 1, 2, 3, …, 9, 10, 20, 30, …, 90, 100. How do we determine where to place them on our scale?
For each value of y that we want to mark on A, there should be a corresponding value of x on D, where x = √y. Thus, the mark on the A scale for y = x2 should be made at a location that is a distance L0 × log(x) = L0 × log(√y) from the left index.
For our A scale, L0 × log(√y) = L0 × log(y1/2) = L0 × (1/2) log(y) = L0/2 × log(y). So, as expected, the A scale is a logarithmic scale for the variable y which has a single-decade length of L0/2. And, of course, the B scale is similarly laid out.
To make our Mannheim set of scales, the layout can be thought of as starting with a scale of “equal parts” — that is, a linear scale — which represents the logarithms of the numbers on the C/D scales. Then using this scale, the layout of the other scales, all of length L0, are created:
C/D scales: marks for values of x, where 1 ≤ x ≤ 10, are made a distance d from the left end of the scale, where d(x) = L0 × log(x).
A/B scales: marks for values of y, where 1 ≤ y ≤ 100, are made a distance d from the left end of the scale, where d(y) = L0 × log(√y) = L0/2 × log(y).
Inverse Functions
In the above construction, we placed marks on a scale of the variable y which itself is a function of x — call it f(x) — where in our case we had y = f(x) = x2. And we found that the marks should be placed at a distance L0 × log(√y) from the left end of the scale. Note that if y = f(x) = x2 then solving for x we get x = √y, which we will call g(y). Here, g is the “inverse function” of the function f(x). The inverse function g “un-does” the operation performed by the original function f. The inverse of the “square” is the “square root”. The inverse of multiplying by 3 is dividing by 3. The inverse of the function log x is the function 10x. If we evaluate f for an input value x we get an answer y; if we put y into the function g, we should x back again. In other words, we have g( f(x) ) = x. In our above example, √(x2) = x.
Note that not all functions have well-defined single-valued inverses. (For example, strictly speaking, if y = x2 then x = +√y or -√y.) But if a reasonable choice can be made for our range of interest — where 1 ≤ x ≤ 10 — then we can contemplate making a slide rule scale for the function. After all, our goal is not just to evaluate a function and read its value, but to use that value in an on-going calculation using the slide rule. A simple rule to remember is that the function should have positive value and should be either continuously increasing or continuously decreasing over the range of x.
So, generally speaking, we find that a mark on the slide rule for a valid value y = f(x) is made at a distance from the left index provided by the inverse of the function f:
Thus if we presume x is a value on the D scale, with a range of 1 ≤ x ≤ 10, then any scale of function f(x) on the slide rule can be made by marking values y on that scale at a distance d(y) = L0 × log[ g(y) ] from the left index, where g is the inverse of f. I am trying to reserve the use of the symbol x to be strictly numbers shown on the D scale (or C scale), and use the symbol y to be a number shown on one of the other scales on the rule.
To make the Mannheim scales:
A/B scales: f(x) = x2, which gives the square of the primary variable x
1 ≤ y ≤ 100
d(y) = L0 × log[ g(y) ] = L0 × log[ y1/2 ]
the inverse function of f(x) = x2 is g(y) = √y
C/D scales: f(x) = x, which defines our primary variable
1 ≤ y ≤ 10
d(y) = L0 × log[ g(y) ] = L0 × log[ y ]
the inverse function1 of f(x) = x is g(y) = y
With a table of logarithms, or a means of computing them, a scale for the function f(x) can be produced for the slide rule through the use of its inverse function, g(y), so long as f(x) has a unique inverse for the range of x being considered.
All of this might appear to be a bit long-winded for such simple scales as the Mannheim set, but the procedure can be used for the development of scales for more general functions, as we will see in a moment.
First, though, I would like to digress for a moment to talk about the Mannheim scales just a bit. This set of scales really enabled the development of the slide rule’s general-purpose computing power, which in turn led to the desire to create new scales to add to that power.
Some Comments on the Mannheim Scales
Historically, the A and B scales on the early slide rules were thought of as the primary scales. Basic multiplication, division, and the evaluation of ratios and proportions were carried out with these scales. When a proportion is set with A and B, one can always see every combination of ratios that corresponds to that setting. On these early rules the D scale was a secondary scale that provided square roots. On the Carpenter’s rules and Soho (Engineer’s) rules of the 1600s and 1700s there was a C scale, but it was just a redundant B scale. This was due to the fact that these slide rules did not have cursors, and so one would carefully set values on B against values on A, and when D was to be used, the values on C (same as on B) could be carefully compared to values on D.
But the Mannheim arrangement replaced the C scale with one equivalent to the D scale on the Engineer’s rule. It also included a cursor, which enabled the careful setting of any scale with any other scale on the rule. With its C scale on the slide, the Mannheim allowed the user to directly multiply or divide by a square at any time during a lengthy calculation — a significant advancement. With this arrangement, calculations such as the following could now be performed with ease (remember, A and B are the main scales):
Note that since B and C slide together, for every number shown on B its square root is carried along on C. Multiplying 2 by 25 on B is the same as multiplying 2 by 52 on C. And so direct multiplication of the square of any number can be performed by using the A and C scales as shown above. And combinations such as a ÷ b × c2 often can be computed in one step:
In addition, after performing a general computation using A and B, the square root of the result can be found immediately using the D scale, as in the following example:
Here we divide 9 on A by 4 on B to get 2.25 on A, and below, on D, we see that its square root is 1.5. The Mannheim arrangement was a very powerful development for its use in general calculations that involve both squares and square roots, and quickly gained international recognition in the late 1800s.
After the Mannheim arrangement was introduced, it did not take long at all before people began to realize that more precision could be obtained in general operations if the C/D scales were used as the primary scales. So eventually these scales were thought of as the “main scales” to produce results x, and the A/B scales could be thought of as functions of x, namely x2 in this case, as we have seen.
Below we will look at some of the other “standard” scales that were developed following the success of the Mannheim arrangement. We’ll see that our formalism involving inverse functions can produce scales for which the results of other functions of x can be created. And in addition, scales for functions that depend upon other variables can also be implemented in a similar way, as for the trigonometric functions of arbitrary angles.
All of our scales below will be generated assuming the scales C and D are marked with values 1 ≤ x ≤ 10, arranged on a standard logarithmic scale.
* Scales With Functions of x *
Logarithm Scale
We actually started our discussion with a linear scale from 0 to 1 which we could use to mark off the distances along the slide rule scales in terms of logarithms. This scale, called the line of equal parts, the line of logarithms, or the logarithm scale is quite often found on a standard slide rule. On early Mannheim slide rules it often was found on the back of the slide and would be labeled as the L scale. As we saw in our very first example above, this L scale provides the logarithms log x of the numbers x found on a C/D scale. Thus, we have values y on the L scale such that y = log x, which inverting yields x = 10y, yielding our inverse function g(y).
L scale: f(x) = log x, hence this scale gives the logarithms of the values x
0 ≤ y ≤ 1
d(y) = L0 × log[ g(y) ] = L0 × log[ 10y ] = L0 × y
the inverse function for y = log x is x = 10y
Inverse or Reciprocal Scale
A common scale added to Mannheim-style slide rules by about 1900 is the inverse scale, or CI.2 The CI yields the reciprocal of values on the C scale. Thus, the scale is laid out such that its marks are placed along log(1/x). But note that if x runs from 1 to 10, then 1/x < 1 and log(1/x) is negative. So, an offset is provided (1 is added to log y) to make the logarithm a positive number that can be placed along the other slide rule scales. This amounts to multiplying 1/x by 10 (log 10/x = log 10 - log x = 1-log x):
CI scale: f(x) = 10/x = 1/x × 10
1 ≤ y ≤ 10
d(y) = L0 × log[ g(y) ] = L0 × log(10/y)
inverting y = 10/x yields x = 10/y
The numbers provided on the CI scale run from right to left. When y = 1, d = L0; when x = 10, d = 0. Besides just reading off reciprocals of numbers, the CI scale is most useful in three-factor multiplication. Since dividing by 1/x is the same as multiplying by x, one can line up b on CI against a on D and then, without moving the slide, find c on C under which one would find a × b × c on D.
Folded Scales
As slide rule users realized that C/D have more precision, they began using them for general purpose calculations instead of A/B. But with C/D, answers often went “off scale”, and the slide needed to be “reset” to complete a calculation. This generated the development of “folded” scales, ones that replicate the C/D scales, but start at the mid-point of a 1-decade log scale. This happens to be at a value of √10. But very soon it was realized that while √10 = 3.162, nearby is 𝜋 = 3.142, which could be considered “close enough” to the mid-point. And so the use of 𝜋 as a starting point quickly became the standard for the CF/DF scales. Marked this way, the CF/DF scales represented multiplying x by 𝜋, a fairly common operation.
When C/D are set for a ratio or a calculation, the result being sought will either be found elsewhere on the C/D scales or, if off-scale on C/D it will be on-scale on the CF/DF scales. And if a result is found on D, say, then 𝜋 times that result will be found directly on DF.
The distances for the marks on the folded scales are thus given by
CF/DF scales: f(x) = 𝜋x
𝜋 ≤ y ≤ 10𝜋
d(y) = L0 × log[ g(y) ] = L0 × log[ y/𝜋 ]
inverting y = 𝜋x yields x = y/𝜋
Early slide rules with CI and CF/DF scales, which are 1-decade long but start at a different phase or starting point, or run the other direction, were named polyphase or maniphase slide rules, particularly by K&E and Dietzgen.
Inverse or Reciprocal Folded Scales
Just as off-scale results on C/D could be found on CF/DF, problems could be worked the other way — multiplication and division could be performed on CF/DF and if the result was off scale on those, it could be found on the C/D scales. And since CI became a useful scale in general multiplication, a CIF scale — an inverse folded scale — was added to complete the set. This allowed for three-factor multiplication and division to be performed using the CF/DF scales.
We want the CIF scale to be the inverse of the folded scales. With an appropriate factor of 10 to give results greater than 1, the distances for the marks on the inverse folded scale CIF are given by
CIF scale: f(x) = 100/(𝜋x) ( = 100 × 1/(𝜋x) )
10/𝜋 ≤ y ≤ 100/𝜋
d(y) = L0 × log[ g(y) ] = L0 × log[ 100/(𝜋y) ]
inverting y = 100/(𝜋x) yields x = 100/(𝜋y)
With the total combination of C/D/CI and CF/DF/CIF, multiplication and division of multiple factors and divisors could be performed in succession without having to do any “reseting” of the slide.
Cubes and Cube Roots
In a similar way as for the A/B scales, a cubic scale can be made by using a 3-decade scale that runs the same length as the C/D scales, as shown here:
For a K scale, marks for values of y = x3, where 1 ≤ x ≤ 10 and thus 1 ≤ y ≤ 1000, are made a distance d from the left end of the scale, where
K scale: f(x) = x3
1 ≤ y ≤ 1000
d(y) = L0 × log[ g(y) ] = L0 × log[ y1/3 ]
inverting y = x3 yields x = y1/3
The values on K are the cubes of the values on D, and the values on D are the cube roots of the values on K. The scale was first introduced in Germany where K stood for “kubisch” and, besides, the “C” label was already taken.
Square Root Scales
While C and D were first envisaged as square root scales for the main scales — which at that time were A and B — they eventually became the dominant scales for computing due to their greater accuracy by a factor of two. In the 1940s and 50s new “square root” scales became available on high end slide rules. Though such scales were found on earlier rules, such as on Excise Officer’s gauging rules in the 1700s and early 1800s, these scales found their way onto more modern slide rules that used various labels, such as the “root scales” R1 and R2 on the Post Versalog, the W1 and W2 scales (and W’1 and W’2) on the Faber-Castell high-end rules, and the “√ ” scales on the high-end Pickett slide rules. Such scales provide the square roots of numbers on the D scale where, for example, R1 interprets D as being from 1 to 10 and R2 interprets D as being from 10 to 100.
For the R1 scale, marks for values of y = x1/2, where 1 ≤ x ≤ 10 and thus 1 ≤ y ≤ 3.162, are made a distance d from the left end of the scale, where
R1 scale: f(x) = x1/2
1 ≤ y ≤ √10
d(y) = L0 × log[ g(y) ] = L0 × log[ y2 ]
inverting y = x1/2 yields x = y2
Then, for the R2 scale, the D scale represents numbers between 10 and 100, or 10 times our “x” variable. Hence, our marks on the scale are for values of (10x)1/2 for 1 ≤ x ≤ 10, and the range for the markings on R2 scale is √10 ≤ y ≤ 10. The marks are made a distance d from the left end of the scale, where
R2 scale: f(x) = (10x)1/2
√10 ≤ y ≤ 10
d(y) = L0 × log[ g(y) ] = L0 × log[ y2/10 ]
inverting y = (10x)1/2 yields x = y2/10
* Functions of Other Variables *
Sine and Tangent Scales
To be able to multiply a number on the D scale with the sine of an angle, we can create a scale that marks off the locations of angles such that when the function is applied to that angle, the result can be read off of the C scale. The distances along the sine scale need to be proportional to the logarithms of the sines of angles so that the scale can participate in multiplication and division calculations.
For example, let’s assume we will want the sine scale to be associated with the C/D scales on a Mannheim rule.3 The sine function oscillates between ±1 in its well-known oscillatory fashion, but we actually want a sine scale, call it S, to cover a single decade as a result of its application. Note that sin(90o) = 1, and sin(5.73o) = 0.1; having an S scale that covers this span of angles is useful in many applications, and so this is what has been adopted on the slide rule. We want to place on our S scale the locations of other angles for which their “sines” can be read on a C/D scale. Let’s designate the distance along our S scale as “d(𝜃)”. Then we want
d(𝜃) = L0 × log[10 × sin(𝜃)], where 5.73o ≤ 𝜃 ≤ 90o
The “10” in the expression above is due to the fact that the sine is always less than 1; thus when 𝜃 = 90o, we have sin 90o = 1, and log(10) = 1, and d = L0 as desired. The sine scale, or S scale, in comparison with a D scale, will look like the following, where the numbers on S are in degrees:
By comparing values x on D with values 𝜃 on S, we can see that
where asin(z) denotes the arcsine of the value z (i.e., the angle whose sine is z). In this sense, each number found on the S scale also can be thought of as a function of the value of x on the C or D scale. The arcsine is sometimes written as “sin-1”. Using our nomenclature for inverse functions,
S scale: f(x) = asin(x/10)
5.73 deg. ≤ 𝜃 ≤ 90 deg.
d(𝜃) = L0 × log[ g(𝜃) ] = L0 × log[ 10 sin 𝜃 ]
inverting y = 𝜃 = asin(x/10) yields x = 10 sin 𝜃
A tangent scale can be created in a similar fashion. For the tangent, we have tan(5.73o) = 0.100 and tan(45o) = 1, so a “T” scale can be made whereby the marks on the scale indicate angles that have tangents equal to the values on a C/D scale:
T scale: f(x) = atan(x/10) (sometimes written as “tan-1(x/10)”)
5.73 deg. ≤ 𝜃 ≤ 45 deg.
d(𝜃) = L0 × log[ g(𝜃) ] = L0 × log[ 10 tan 𝜃 ]
inverting y = 𝜃 = atan(x/10) yields x = 10 tan 𝜃
If our logarithmic S and T scales are located on the slide, then they can be used directly with the D scale to multiply and divide values of sines and tangents in general calculations, as shown in the following figures:
In the middle of the 20th century, scientists and engineers began working with angles often expressed in radians rather than in degrees, and so some S and T scales had markings in these units. The scales would be made using the same functions f as above, but the values of y would have limits of
S scale: L0 × log[ g(y) ], where 0.100 ≤ y ≤ 1.57 = 𝜋/2 radians
T scale: L0 × log[ g(y) ], where 0.100 ≤ y ≤ 0.785 = 𝜋/4 radians
For angles less than about 5.73 degrees, the sine and tangent functions have roughly the same values. An angle of 5.73 degrees has a tangent of 0.1003 and a sine of 0.0998. This difference — 0.0005 — is at or below the limit of accurate readings for the standard 25 cm slide rule, and the difference continues to diminish for smaller angles. So, for such small angles a new scale was formed call ST (sine/tangent for small angles) and runs linearly from x = 0.01 on the left to x = 0.1 on the right, which are marked by angles starting at 0.573 degrees on the left and ending at 5.73 degrees on the right.
ST scale: f(x) = 0.573x
0.573 deg. ≤ 𝜃 ≤ 5.73 deg.
d(y) = L0 × log[ g(y) ] = L0 × log(y/0.573)
inverting y = 𝜃 = 0.573x yields x = 𝜃/0.573 (𝜃 in degrees)
If angles are expressed in radians, then for very small angles such as these,
and this is seen on the scales, since there are 180/𝜋 = 57.30 degrees in a radian. Since the ST scale is linear, and it starts at a value of 0.573, then it is akin to the Folded Scales in that it multiplies values on D by the factor 0.573, rather than by 𝜋. If we think of values on C/D as in radians, then the ST scale can provide a conversion from radians to degrees. For instance, if an angle of 0.68 radians is found on C/D (read 6.8) then we would find 39 degrees on ST ( read 3.9).
For this reason some manufacturers began to label the ST scale as “SRT” to emphasize this functionality.
* Log-Log Scales *
Our final set of scales found on many slide rules is that of the Log-Log scales. These scales are independent of the other scales on the slide rule; they are not generally used in multiplication and division calculations, though some special circumstances permit this to happen. The Log-Logs are special scales used for finding values of general numbers raised to general powers. Their use comes from two properties of logarithms:
log (a×b) = log a + log b
log( bx ) = x × log b
Taking the log of the second property and employing the first property on the result, we see that
log[ log( bx ) ] = log( x × log b ) = log x + log(log b)
Our slide rules have a C scale on the slide which is drawn proportional to log x. By creating Log-Log scales for which we find a value of log(log b) we can add log x to values of log(log b) in order to locate the the value of log(log bx). For more on this topic take a look at this post.
But I need to point out that the “log” in our “log b” above could, in fact, be the natural logarithm, ln(b), which is the logarithm using base e = 2.718. That is, the following is also true through the same argument as above:
This is actually the most common form used on the modern slide rules. A few mid-century rules, such as the Pickett Models 2, 3, and 4, used only Base-10 logs for their Log-Log scales. On these slide rules, the Log-Log scales are denoted as “N” scales. On most other slide rules, the scales are denoted by “LL”, or perhaps by “Ln” scale labels, and use the mixed-base set of log-ln, which we will describe below. Whether log-log or log-ln, such scales are all called “Log-Log” scales.
To create the mixed-base Log-Log scales, the distance from the left end of a scale to the number marked y will be d(y) = L0 × log( ln y ). Note that the number on the left end of the scale will not be “1”, nor will it end with a factor of 10. If the number x on the D scale is compared to the number y marked on the LL scale at the same distance along the scales, we find that
A value y that appears on the LL scale is the exponential of the corresponding x on the D scale! Going the other way, the scales show us that the value x on the D scale is the natural logarithm of the value y on the LL scale. (This is because ln x and ex are inverse functions of each other.) It was this realization that led to the use of the mixed-base “log-ln” Log-Log scales for general bx calculations, as it adds more computational functionality to the rule, allowing exponentials and natural logarithms to be obtained.
In our present example, where d(y) = L0 × log( ln y ) = L0 × log( ln ex ), we can compare this to our previous scalings in terms of a function f and its inverse:
LL scales: f(x) = ex
e1 ≤ y ≤ e10
d(y) = L0 × log[ g(y) ] = L0 × log[ ln y ]
inverting y = ex yields x = ln y
As the D scale runs from 1 to 10 then the LL scale would run from a value of e1 = 2.718 on the left end, to e10 = 22,026 on the right end. But we could also interpret the end values of our 1-decade-long C and D scales as 0.1-1, or perhaps from 0.01-0.1, or even 0.001-0.01, say. In these cases, the numbers shown at the limits of our LL scale would be adjusted accordingly. So for x on the D scale we can make a scale that computes y = ex/100, for instance. To find the required inverse:
So what we find is that the slide rules tended to have 3 or 4 scales, which were labeled typically as shown below, where y = ex:
LL0 — range e0.001 ≤ y ≤ e0.01: d(y) = L0 × log[ 1000 ln(y) ]
LL1 — range e0.01 ≤ y ≤ e0.1: d(y) = L0 × log[ 100 ln(y) ]
LL2 — range e0.1 ≤ y ≤ e1: d(y) = L0 × log[ 10 ln(y) ]
LL3 — range e1 ≤ y ≤ e10: d(y) = L0 × log[ ln(y) ]
Here is an image showing scales using these functions, along with a standard D scale:
From this image, note that with the index of D lined up against a value on the LL scale, say 2.718, then finding 3 on the D scale, one can find (2.718)3 directly below on the LL3 scale — here, about 20. Using C, which is on the slide of the slide rule, the operation can be performed starting with the other numbers on the LL scales.
The LL0-LL3 scales are used to take a number greater than 1 and raise it to a power; the result will always be greater than 1 as well. For raising numbers less than 1 to powers, the LL00-LL03 scales are used. These are essentially reciprocals of the original LL scales. And, in terms of exponentials, they provide values of y = e-x.
For 1 ≤ x ≤ 10 on the D scale, if y = e-x then x = -ln y. The minus sign is just fine, as the natural logarithms of numbers less than 1 are themselves negative. And so our marks for the LL00-03 scales are made as follows:
LL00 — range e-0.001 ≤ y ≤ e-0.01: d(y) = L0 × log[ -1000 ln(y) ]
LL01 — range e-0.01 ≤ y ≤ e-0.1: d(y) = L0 × log[ -100 ln(y) ]
LL02 — range e-0.1 ≤ y ≤ e-1: d(y) = L0 × log[ -10 ln(y) ]
LL03 — range e-1 ≤ y ≤ e-10: d(y) = L0 × log[ -ln(y) ]
You’ll notice that the distances d(y) for ex and for e-x are equivalent. Also, since the values of y are the inverses of their partners on the LL0-3 scales, the values of y on the LL00-03 scales run right to left. The scales operate in the same way using the C scale, however. Raising a number less than 1 to a positive power results in an even smaller number. Here is an image showing scales using these functions, along with a standard D scale:
In all of the above we have been talking about what I would call “standard” slide rule scales, which is to say that these are the more modern versions of the commonly found scales that developed after centuries of use. There are certainly variations, particularly with older slide rules.4 And the list of scales is not meant to be exhaustive, though it was a bit exhausting writing this up. But hopefully our discussion can get one started on the general understanding and use of linear Mannheim-style slide rules — and even circular slide rules, in a similar way — and the procedures for creating the scales found upon them. By the way, it was not my intent when I started this, but I seem to have described all of the scales found on the Post Versalog II slide rule.
Summary of Standard Scale Making
The main scales for computing are taken to be C/D scales which run from 1 to 10. These and the other scales on the slide rule are assumed to have the same physical length, L0.
For each scale, values of y are chosen to be marked. The table below shows the minimum and maximum acceptable values of y for each scale. In terms of the variable x that appears on the C/D scales, other scales represent functions of x, denoted by f(x). Both f and its inverse g are shown in the table.
The marks for values y to be made on each scale are chosen, and then placed at a distance d from the left end, according to the inverse function:
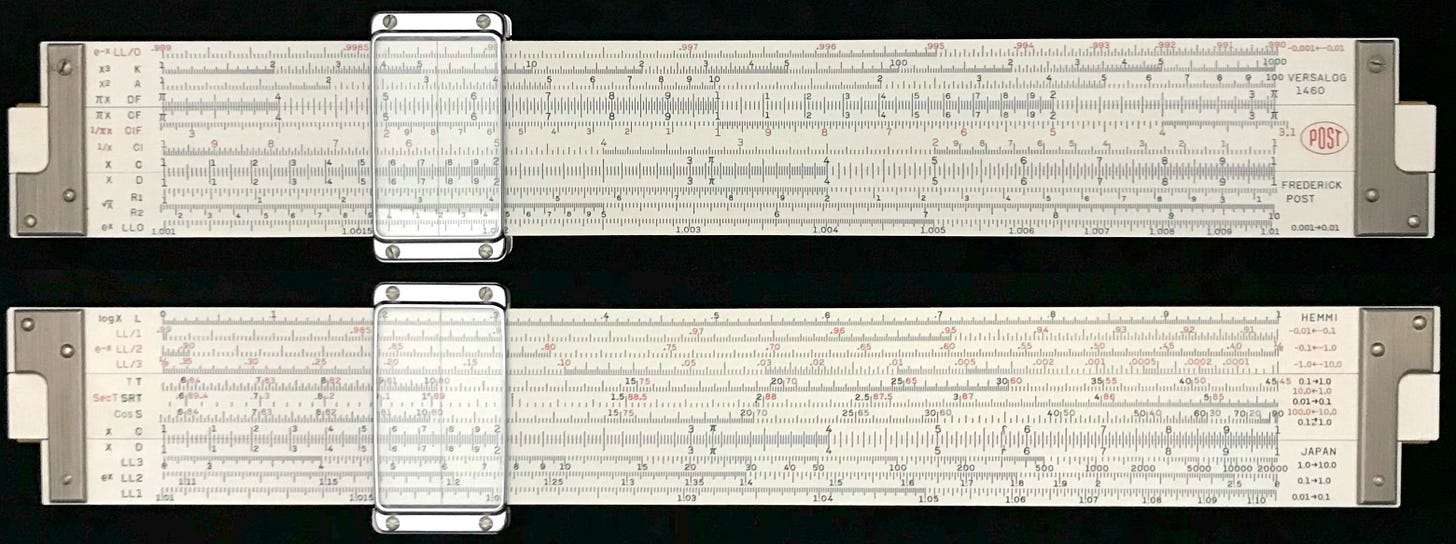
In our next couple of posts we will provide some sample computer code that, in conjunction with the information in the above table, can be used to create the standard scales that we have been discussing. The functions and code snippets in the upcoming posts were used to generate the scales shown in the images of this article. And we will go through an example or two where we create slide rule scales of our own user-supplied functions to illustrate the process.
It always sounds funny to write that the inverse function of f(x) = x is g(y) = y. But if we put a value, say “3”, into f, we get 3. And if we take that value and put it into g, we get 3, which, indeed, is what we started with.
Occasionally one might find a DI scale — same principle, though not as common. The CI scale is found on the slide of the slide rule, while when the same scale is found on the “stock” of the slide rule, it is labeled DI.
The earliest Mannheim rules often had sine scales on the back of the slide, and they were typically associated with the A/B scales — that is, the sine scale went from 0.01 (corresponding to about 0.57 degrees) to 1 (corresponding to 90 degrees). By the mid-1900s the trig scales were typically associated with the C/D scales for their improved accuracy.
For example, in 1909 K&E introduced the first Log-Log slide rule made in the U.S., the model 4092, with the first three-segment set of scales, LL1, LL2, and LL3. In 1922 K&E revamped the rule and added a scale “LL0” to its new 4092-3 (and 4092-5). But the “LL0” on this rule was actually a special 2-decade folded log-log scale which essentially was a hybrid of the future LL01 and LL02 scales. It used the B scale to add values of log x to log by on its special “LL0” scale. This model was discontinued in 1937. The new K&E LogLog slide rules — the 4080 and 4081 — divided and expanded the old “LL0” scale into a new set, the “LL0” and “LL00” scales. These still used B, but the “LL0” contained what would become the future LL00 and LL01 scales on one line. Its “LL00” scale consisted of the future LL02 and LL03 scales on one line. Finally, in about 1950, these models were revamped and had the now-standard LogLog scales LL1-3 and LL01-03, all of which used the C scale for calculations.























Insightful comments even on basic Mannheim scales.
Just fantastic.
Zowie, a tour-de-force!