So far in our three-part series we have looked at the use of 2-dimensional curves — circles, a series of concentric circles, and spirals — for producing longer logarithmic scales for use in adding and subtracting logarithms on a “circular” slide rule to obtain higher precision. We discussed how the variable that changes logarithmically in such a system is the angle of rotation, 𝜃, and not necessarily the distance, s, along the path. But the total length of the scale used to add logarithms is still a very good indicator of the accuracy that the slide rule can provide.
Compared to a linear slide rule scale of length d, a scale placed on a single circle of diameter d will have a scale length 𝜋 times longer. And by using either a set of concentric circles or a pure spiral curve, where radii of the curves get larger with increasing angle, then the distribution of marked numbers over N rotations can be spread out even more, providing further enhancements to accuracy of calculations. In such slide rules we found that the total path length is enhanced by a factor of about N/2 compared to a single circle of the same outer diameter. On the other hand, the accuracy of settings and readings at larger radii on such a scale will still be slightly better than the performance at smaller radii.
But rather than having circles or spirals that increase their radii from smaller to larger values, what if we had a series of N circles that each have the same diameter d. This, in principle, could yield another factor of two in total path length, which would now become s = N × 𝜋d. A very good approximation to such a situation is a tightly-wound helical curve placed upon a cylindrical surface.
Helical Logarithmic Scales
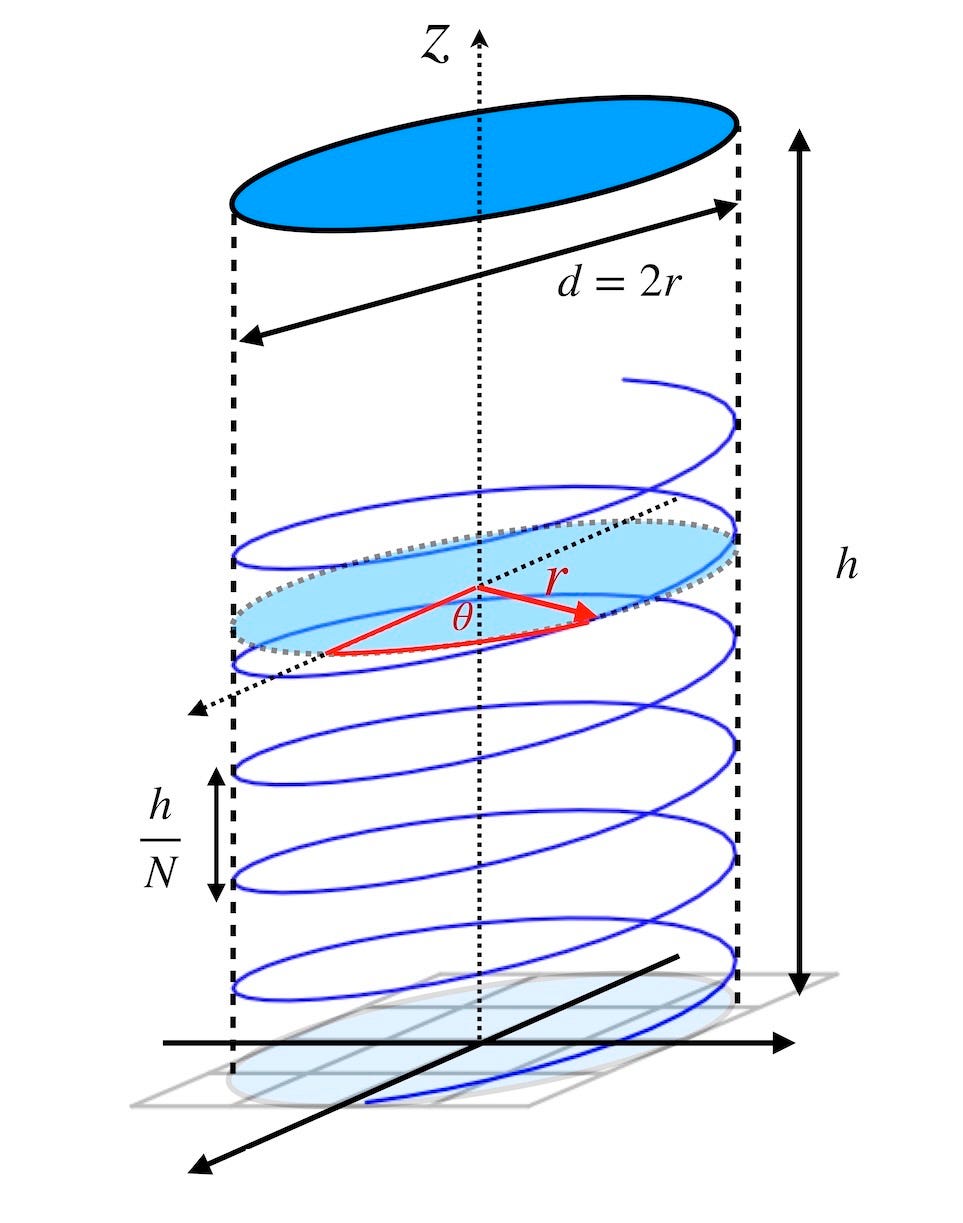
Let’s look at a helix drawn on a cylindrical surface. Let d = 2r be the diameter of the cylinder, h is the total length of the cylinder’s axis, and θ is the angle of rotation about that axis. To make a helix, we imagine a point rotating in circular fashion with constant frequency, but the center of the circle moves at a constant rate perpendicular to the circular motion. The configuration is illustrated in the figure below.
As the center of the circle moves along the z axis, the angle θ rotates at a constant rate that is proportional to the advancement of z. The curve thus moves with constant radius, r, along the surface of the cylinder. Suppose the helix performs N total rotations over the total length h. The total θ after N rotations would be N× 2π, while the total advancement of z would be h. Thus, the angle θ must be related to z by the following equation:
Imagine that we slice the surface of the cylinder along a line parallel to the axis, and then “un-roll” the cylindrical surface to form a flat plane. Here is the pattern that emerges:

The numbers marked along the length of the curve on our helical slide rule follow a standard logarithmic scale, beginning at 1 at the bottom left and ending at 10 at the top right. Each line is separated from its neighbors by a distance h/N. And the physical distance along the horizontal axis in the image above will be the circumference of the cylinder, πd. Thus, the total length along one of our N lines above can be calculated using the Pythagorean Theorem, namely
Finally, over a total of N spirals, we have a total length of N times this result, or
If there is a large number of spirals and if the device is constructed such that its length h and its diameter d are approximately of the same size, then the second term under the radical sign will be much, much smaller than 1, and the above expression for the final scale length reduces to an approximate value of Nπd. (Note that this essentially approximates the helix as N circles each of diameter d.) As an example, a one-inch diameter cylinder with a 30-turn helix will have a scale with an effective length of about 100 inches. This is ten times longer than the standard 10-inch slide rule, yet the helical slide rule likely can still fit in a coat pocket.
Taking a scale such as the one above, rolled onto a cylinder, one now just needs to have a method for adding distances along the scale in order to perform multiplication calculations. So, one needs a device that can slide scales or indicators up and down along the axis, but that can also rotate the scale or rotate an indicator in order to read results along the helical curve. Various such methods exist, and depend upon the design of the particular slide rule, but the fundamental principle is the same as for any other slide rule – adding distances along the logarithmic scale provides a multiplication calculation.
When moving an indicator for the value x along the spiral curve on the outside of the cylinder, one is simultaneously moving the position of the indicator along the axis of the device as well as rotating the angle θ. If the logarithmic scale for x begins at z = θ = 0 when x = 1, and ends at z = h, θ = 2πN when x = 10, then we have
There were helical slide rules manufactured by McFarlane (Scotland), Stanley (London), Otis King (London), Browne (Melbourne) and others. Below we will examine the Otis King, perhaps the most popular, as well as the Fuller Calculating Slide Rule by Stanley with its very long scale.
The Otis King
The Otis King’s Calculator, manufactured by Carbic Limited, London, was produced from 1921 until 1972. The patent for the device filed by Otis Carter Formby King in 1921 was accepted in August, 1922.1 The original models produced by Carbic (Models A-J) were made for business usage such as retail cash and wage calculations and are quite rare;2 but Models K and L were more generic and became popular for a wide variety of applications where greater computational accuracy was required.
Each model consists of a thin base cylinder with a stainless steel handle from within which a rotatable cylinder of slightly smaller diameter can be extended by about 4 inches. This inner cylinder can be rotated using a “knob” at its end. When the inner cylinder is collapsed within the outer cylinder, the total length of the slide rule is about 6 in.
The base cylinder of the Model K has an outer diameter of about d = 1.05 in, and just above its handle begins a single-decade logarithmic helical scale. The total height of this scale on the cylinder is h = 2 in and contains N = 20 turns. Approximately 1.25 in above this single-decade scale is a two-decade scale, also of 20 turns per decade and with a total height of 4 in (2 in per decade).
The Model L has the same outside dimensions when closed as the Model K, but the scales on the inside cylinders are slightly different. The base cylinder of the Model L is essentially the same one-decade helical logarithmic scale; however, the two-decade scale is replaced by a one-decade scale plus a linear scale along a helix of the same total length. The top and bottom log scales can be used for multiplications, while the linear scale provides the logarithms of the numbers on the log scales, thus allowing for calculations involving raising numbers to powers, etc.
Using the parameters provided above, we can compute the effective length of the logarithmic scales found on the Otis Kings:
The Otis King was popular for many years due to its fine construction and its ease of use, as well as its accuracy. To perform a multiplication (using the Model K, for instance),
Fully extend the inner cylinder to expose the entire scale.
Move the black cylinder down until its white dot at the bottom lines up with the first number, a.
Holding the knob at the top of the slide rule, and not moving the black cylinder, set the middle “1” on the helical scale to the white dot at the top of the black cylinder.
Moving the black cylinder only, align its top white dot with the second number, b.
Note: b will be accessible by either moving up or by moving down, which is why we start by aligning on the “middle 1”.
The product a×b is then found at the white dot at the bottom of the black cylinder.
If this series of movements is studied for a moment one can see that we are simply adding distances along the axis of the slide rule – which are proportional to the logarithms of numbers – and hence performing the exact same calculation that are performed on a standard linear slide rule.
Further information and examples of calculations can be found in the Otis King instructions sheet.
For more information on the Otis King Calculators:
Peter Hopp, “Otis-King Update”, Jour. Oughtred Soc., Vol4.2 (1995) p33.
Peter Hopp, “Otis-King - Conclusions?”, Jour. Oughtred Soc., Vol5.2 (1996) p62.
R.C. Blankenhorn, “The Otis King’s Patent Calculators - Catalogue Raisonne”, Jour. Oughtred Soc., Vol18.1 (2009) p49.
Peter M. Hopp, Slide Rules – Their History, Models, and Makers, Astragal Press (1999) pp.112,150,
Dick Lyon, Otis King’s Patent Calculator, http://www.svpal.org/~dickel/OK/OtisKing.html.
International Slide Rule Museum, https://sliderulemuseum.com/British.htm.
The Fuller Calculator
The Fuller Calculator is a helical slide rule that was manufactured beginning in 1878 and various incarnations were sold for almost 100 years. There were two primary models (curiously named the Model 1 and the Model 2) and a few not-so-common models. Model 1 has a single helical scale for doing straightforward multiplication and division calculations. The Model 2 in addition has scales for sines and logarithms on its inner cylinder. A Model 3 “Fuller-Bakewell” also exists, which contains scales of sin𝜃 cos𝜃 and cos2𝜃 for use in stadia calculations, and there were special slide rules for coordinate transformations and for complex number multiplications. However, the Model 1 was the most popular and I’m fortunate to have a Model 1 from 1909.
Our Fuller Model 1, which is labeled “Fuller’s Spiral Slide Rule”, was obtained from a bank in New Jersey, where they were “cleaning out the closet”. It has a frame made of mahogany, including its solid handle. Many of the more modern Fullers have a hole in the end of the handle which allowed for it to be placed into a rod to hold the slide rule up at an angle for the user. This early model has no such hole, and its early wooden box allows for the handle to protrude out the end of the box,3 while later models had boxes that surrounded the handle as well as the cylinder attached to it.
The main outer cylinder of the slide rule has a diameter of approximately d = 3.2 inches and its scale has a total height of h = 5.5 inches. The helix goes through a total of N = 50 rotations. Thus, the total length of the single-decade logarithmic scale on the slide rule is
Since it is 50 times longer than the length of the standard 10-inch slide rule, the Fuller was able to compute answers to four significant figures without difficulty, and in many circumstances to five significant figures.
In addition to the 500-inch helical scale, there is a single-turn linear scale at the top of the outer cylinder which goes from 000 to 020, the “000” being aligned with the “1” on the helix. Since there are 50 turns in the helix, each turn around the cylinder increases the logarithm of a number by 0.02. So, by keeping track of what “turn” a number is on and by reading off the number on the circular “020” scale, the logarithm of any number on the helix can be found to approximately 4 significant figures. Counting the turn number is performed using a special scale along the major cursor of the slide rule, which runs from 0 to 100 in 0.02 gradation.
The Fuller uses two cursors to perform calculations. The longest cursor has two indicators A and B, one at the bottom end of the cursor (B) and one roughly midway down the cursor (A). This long cursor is attached to the top of the slide rule (the handle being at the bottom). This cursor can also be rotated independent of the base and of the main cylinder containing the logarithmic scale. Then, there is another, shorter cursor which is attached directly to the base of the slide rule. This cursor has a free “tip” which is referred to as indicator F (for “fixed”). If the scaled cylinder is moved to the bottom of the rule, then F can be aligned with 1 on the scale; if the cylinder is moved to the top of the rule, then F can be aligned with 10 on the scale.
To illustrate a basic multiplication calculation on the Fuller calculator, let’s take 173 times 24 to get 4152. We set the number 173 onto the fixed indicator, F. We then bring either the A or B indicators to either the 1 or 10 on the scale, whichever can be performed. (Like any slide rule, a number might go “off-scale” in one direction or the other.) In our case, we move the A to 1 (and the B makes it to 10). Then, we leave the indicators alone, and move the cylinder to line up 24 on the A or B indicators (A in our case).
The result will be found at the fixed indicator, F: 4152.
Again, if you carefully rexamine this series of movements you’ll be able to see that we are simply adding distances along the axis of the slide rule which are proportional to the logarithms of the numbers of interest.
To find the logarithm of a number using the Fuller, let’s take the log of our result above. Naturally, the log of 4152 is the same as 3 plus the log of 4.152. Keeping that in mind, we slide the cylinder toward the top of the rule, and rotate it to align the number 4.152 with the A indicator. From our “020” scale, we see that the long brass cursor passes by the number 0183. We also note that the fractional number at the top of this cursor that lines up with the top line of the spiral scale is “0.60”. This tells us that the log of 4.152 = 0.60 (from the number of turns) + 0.0183 (from the fractional rotation) = 0.6182. Hence, the log of 4152 will be 3.6183. Let’s check by computer:
log(4152) = 3.618257.
Rather than going on with many other examples, the reader is referred to the well-written instructions that came with the Fuller Calculator.
Further information on the Fuller Calculators can be found at:
Wayne Feely and Conrad Schure, “The Fuller Calculating Instrument”, Jour. Oughtred Soc. Vol 4.2 (1995) p33.
Wayne Feely and Conrad Schure, “Update of Known Fuller and Thacher Rules”, Jour. Oughtred Soc. Vol 5.1 (1996) p25.
Peter M. Hopp, Slide Rules – Their History, Models, and Makers, Astragal Press (1999) pp.113-114,221.
Wikipedia, Fuller Calculator, https://en.wikipedia.org/wiki/Fuller_calculator.
Some Comments on Accuracy
Again, as with the spiral curve, the logarithmic scale for our main variable x is related to the total angle of rotation, θ = 2πN log x. But as the rotation angle varies so does the distance along the axis: z = h (θ/2πN) = h log x. Taking our earlier image of an “unfolded” cylinder, we see that the distance along the helical curve must also vary in this way:
And so, the relative error for settings along the entire length of the helical scale is constant, and inversely proportional to the total length, Leq, of the helical path, akin to our result for a linear slide rule:
Wrapping it up
Over the past three posts we have examined a few methods used to increase the effective length of a slide rule to be able to add and subtract logarithms with greater precision. Using circular, spiral, and helical paths, total scale lengths could be compressed into smaller areas yielding more computing power in the same space, or the same computing power in a smaller space. Such scales used an angle rather than a distance as the logarithmic variable, which was used to yield the markings along the path. So by adding angles of rotation logarithms could be added to provide a multiplication.
Compared to a linear logarithmic scale of length d, the effective lengths, s, of the scales of our other example slide rules are summarized below.
Linear scale of length d:
\(s = d\)
Circular scale of diameter d:
\(s = \pi d\)Set of N equally spaced concentric circles, outer scale diameter d, inner scale diameter di:
\(\begin{eqnarray*} s &=& N\pi\; \frac{d_i+d}{2} \\ &=& \frac{N}{2}\;\pi d ~~\times~~ (1+d_i/d) \end{eqnarray*}\)Spiral scale with N turns, outer diameter d, inner diameter di, with k = (d-di)/(4𝜋N):
\(\begin{eqnarray*} s &=& \frac{1}{4} \left[ d \sqrt{1+d^2/4k^2} - d_i \sqrt{1+d_i^2/4k^2} + 2k\cdot\ln\left(\frac{d/2k + \sqrt{1+d^2/4k^2}}{d_i/2k + \sqrt{1+d_i^2/4k^2}} \right) \right] \\ &\approx& \frac{1}{4}\frac{2\pi N}{(d-d_i)} (d^2-d_i^2) + \frac{1}{4}\frac{(d-d_i)}{2\pi N}\;\ln\left(\frac{d}{d_i}\right) \\ &\approx& \frac{N}{2}\;\pi d ~~\times~~ (1+d_i/d) \end{eqnarray*}\)Helical scale with N turns, diameter d, length h:
The relative error of results found on a linear slide rule varies with the inverse of the path length, and the same is true for single-turn circular slide rules and for helical logarithmic scales. When using concentric multi-turn circular rules or spiral slide rules, the relative error also varies roughly with the inverse of the path length, but readings and settings performed at smaller radii will have a bit less accuracy than those performed at the larger radii, though not by very large factors in general.
As buildings reached heights nearing 100 stories, bridges across rivers became miles long, industries making millions of widgets needed to make ever better estimates for their production, and so on, the need for higher accuracy and more reliable numerical results grew over the twentieth century, and the circular, spiral, and helical slide rules helped to provide the answers.
And then again, sometimes people just wanted to be able to carry the power of a desktop slide rule in their coat pocket. How cool must that have felt?
Peter M. Hopp, Slide Rules – Their History, Models, and Makers, Astragal Press (1999) p. 150.
The hole in the end of this box was likely added later by an owner. The handle unscrews from the cylinder and originally would have been detached and stored in the box.