Trigonometry on the Slide Rule

The S, T, and ST scales

Trigonometry has had its place in many disciplines such as navigation, surveying, astronomy, and so on. At the time of the early slide rules, the need for multiplying distances with values of trigonometric functions was driven mostly by sea navigation, as well as astronomical calculations in celestial mechanics. Even Napier’s original tables of logarithms contained the logarithms for values of the trigonometric functions, as mariners needed to multiply distances by the sine, cosine, or tangent of angles when determining one’s location or when plotting a course. So by the time Mannheim slide rules were first developed in the mid-1800s, the inclusion of sine and tangent scales was almost immediate.

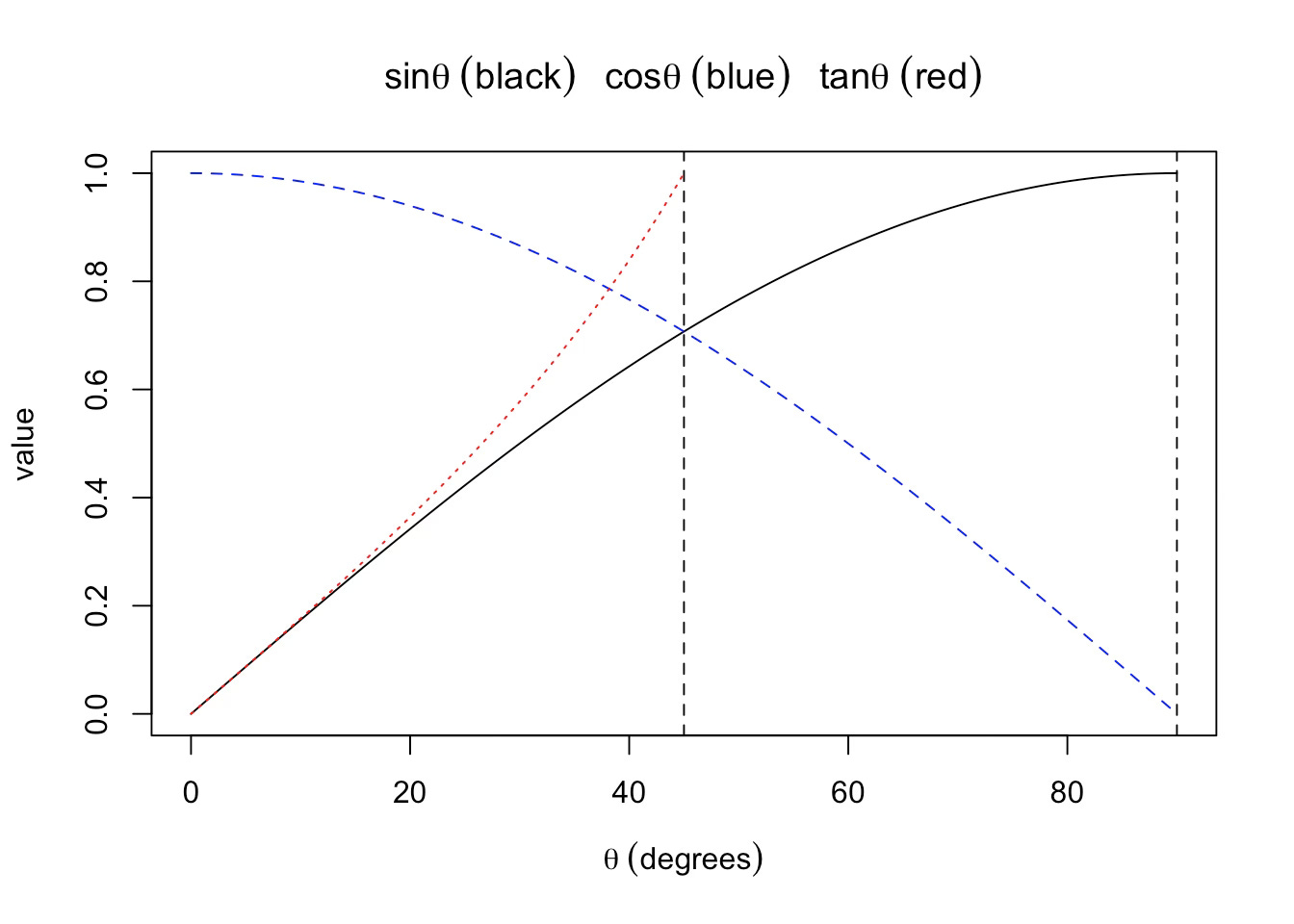
As can be seen in the image above, the modern trigonometric functions are defined in terms of distances found in a right-triangle inscribed within a circle of unit radius. I say “modern” as there were slight variations of such definitions over the centuries, and other functions defined as well, such as the haversine function.¹ If we look at values of the sine, cosine, and tangent as a function of angle, we get the following:

Plot of standard trigonometric functions. The vertical dashed lines are at θ = 45 and 90 degrees.

We want scales of trigonometric functions that can be useful on a slide rule. For instance, if the C and D scales are used for primary multiplication and division, then we can imagine a scale, labeled S, that is proportional to the logarithms of the sines of angles. If we interpret C/D as running from 0.1 to 1, then on such an S scale the value of 1 would correspond to an angle of 90 degrees, while the value of 0.1 would correspond to an angle of about 5.7 degrees. Interestingly, since for small angles the cosine has a value of approximately 1, then the tangent and the sine have approximately equal values at 5.7 degrees and below. But the tangent has a value of 1 when the angle is 45 degrees, thus giving the limits of the angles found on the tangent (T) scale. An example of such scales on a slide rule is illustrated below:

Pickett N600-T slide rule, with S, T, and ST scales associated with C/D scales.

Note that there is no cosine scale, as the cosine of A degrees is the same as the sine of (90-A) degrees. Thus, the S scale can be used with this relationship in mind. Some of the more modern slide rules have the complementary angles marked on the S scale in a different color or perhaps italicized. Above, the S scale has two sets of numbers, the red numbers being the black numbers subtracted from 90.²

To create an S scale on the rule, we take an angle A and place our mark a distance proportional to log( sin A ) from the left end of the C scale. If we then move the left index to a value x on the D scale, then under the A mark on S we would find on D the value of x times sin A. Here is an example of multiplying 2.2 times the sine of 15 degrees to get 0.569:

Calculation of 2.2 ╳ sin(15 deg) .

Most slide rules from the early 1900s and later have S and T scales that correspond to values of 0.1 to 1 on the D scale. But sometimes, especially on older rules, trig values may be meant to be read off of the A scale, which runs from 0.01 to 0.1 to 1. This is because the users of the earlier rules were trained to do their primary calculations (usually in terms of ratios) on the A/B scales. For such older rules, the S scale will be marked from about 0.57 degrees on the left to 5.7 degrees at the middle to 90 degrees on the right. But as the C and D scales came to be used more for primary calculations due to their greater accuracy, the trig scales began to be associated with these instead.

DMS, Decimal Degrees, Grads, and Radians

The earliest slide rules had angles marked off in degrees, minutes (1/60 of a degree) and seconds (1/60 of a minute). More modern rules used decimal degrees rather than the antiquated minutes and seconds of arc, and hence slide rule brands such as “Deci-Trig” began to appear. Very occasionally, one might come across a slide rule, particularly one from Europe, where the S and T scales are in units of grad (or grade, or gons) which, in line with the metric system, is defined as one one-hundredth of a right angle. That is, 90 degrees = 100 g. In this case, the S scale would end at 100 instead of 90, and the T scale would end at 50 rather than 45. Additionally, in the mid-1900s, the use of radians rather than degrees to describe angles became more common with many engineers and scientists. In a complete circle there will be 360 degrees or 2π radians. There were some specialty slide rules for which radians were specifically used for trig. But more common was the use of the ST scale to convert between the two.

The ST or SRT Scale

The C and D scales can provide values for S and T that range from about 5.7 degrees up to 90 or 45 deg on S or T. But when A and B are related to S or T, the range for the function’s value goes down to 0.01, or an angle of about 0.57 deg. To have the same range on modern slide rules with trig scales related to C and D, a separate scale was created with a range of angles from about 0.57 deg to 5.7 deg, interpreting D as from 0.01 to 0.1. This scale is designated as the ST scale. Of course scales with the DMS markings would have 34’ (34 minutes of arc) on the left, up to about 5 deg 42’ on the right.

Now notice that for such small angles where the sine and tangent functions are approximately equal, their values are essentially equal to the angle when expressed in radians, since sin x = tan x = x for small angles expressed in radians. So if the ST scale is marked in units of degrees, and its value is read on the C scale, say, which is dimensionless, then this scale can be used as a conversion scale between degrees and radians. Remember that 1 radian is equivalent to 180/𝛑 = 57.3 degrees. And so one can find scales marked SRT, rather than ST, to emphasize this property of the scale.

Right Triangles and the P (Pythagorian) Scale

Some of the advanced slide rules, particularly form Europe, may have a special scale usually labeled P (or, Pythagorean scale) that gives the value of

\(\sqrt{1-x^2}\)

for a given value of x on the D scale. This is a common operation for certain other computational problems, but noting that

\(|\cos x | = \sqrt{1-\sin^2 x}\)

means that one can use this scale to quickly find the cosine of an angle. An example of a rule with a P scale is provided here:

Faber-Castell slide rule with a “P” Scale.

The cursor in the figure above is aligned with the 40 degree mark on the S scale. We see that the sine of this angle is 0.643 (on the D scale). On the P scale we can read off the cosine of this angle as 0.766. This is only one use of the P scale. While P is not a common scale among the American-made slide rules, we may talk someday about some of its other more common uses.

---

We’ve now covered many of the basic scales that are found on most slide rules. Scientists, engineers, bankers, students, all learned how to use these scales for their work. There are a couple of others that we’ll get to in time, such as the “log-log” scales, which are just a bit more advanced. But next time we should start getting into the variety of slide rules produced during the past couple of centuries and where to find them.

---

---

1. In terms of the modern functions, the haversine was defined as hav x = (1-cos x)/2.

2. The T scale on this particular slide rule also has angles in red that are 90 minus the black numbers on the scale. The values of the tangent for angles between 45 and about 84 degrees in red on this scale are associated with the DI scale on this slide rule.